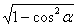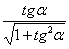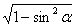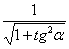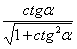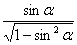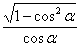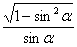3. Тригонометрические зависимости 

4. Тригонометрические формулы приведения

5. Выражение одной тригонометрической функции через другую функцию того же угла

Основные тригонометрические формулы:

sin²α + cos²α = 1;

sin(α ± β) = sinαcosβ ± cosαsinβ;

cos(a ± β) = cosα cosβ ± sinα sinβ;

tg(α ± β) = (tgα ± tgβ) = (1 ± tgα tgβ);

ctg(α ± β) = (ctgα ctgβ ± 1) = (ctgβ ± ctgα);

sin2α = 2sinα cosα = 2/(ctgα + tgα);

cos2α = cos²α - sin²α = 1 - 2sin²α = 2cos²α - 1;

tg2α = 2tgα/(1 - tg²α) = 2/(ctgα – tgα);

ctg2α = (ctg²α – 1)/(2ctgα) = (1/2)(ctgα - tgα);

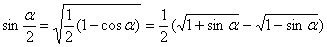
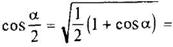
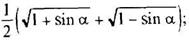
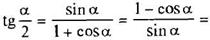
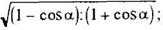
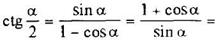
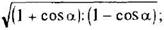
2sin²α = 1 – cos2α;

2cos²α = 1 + cos2α.