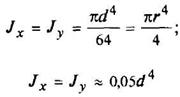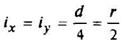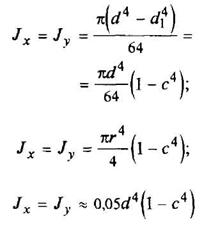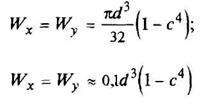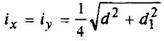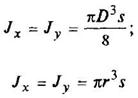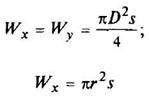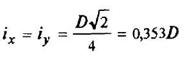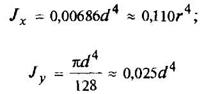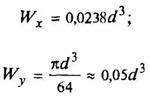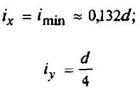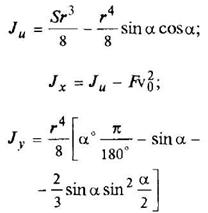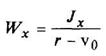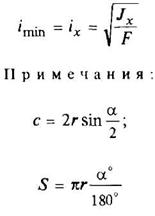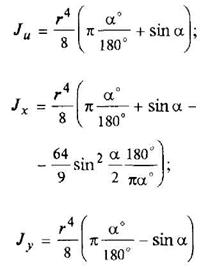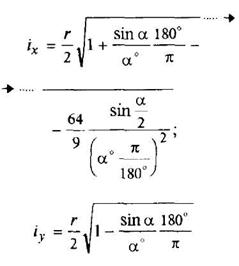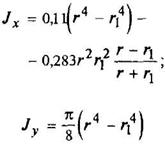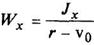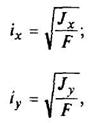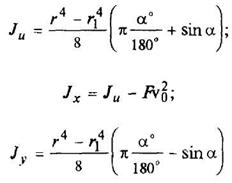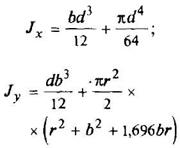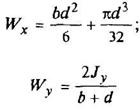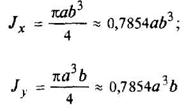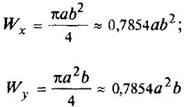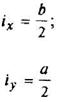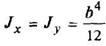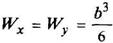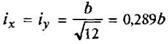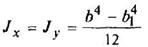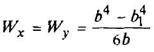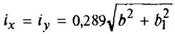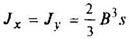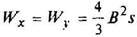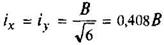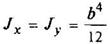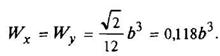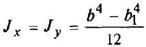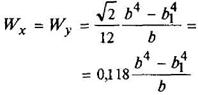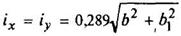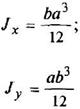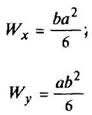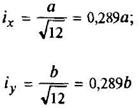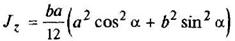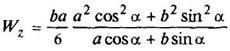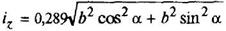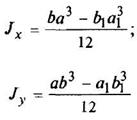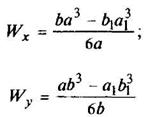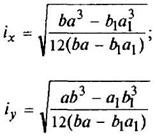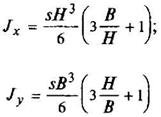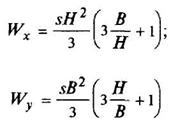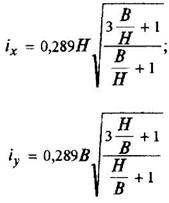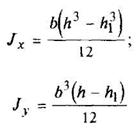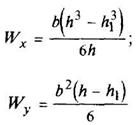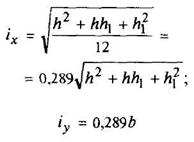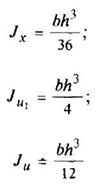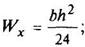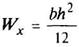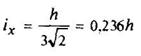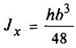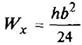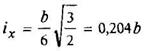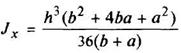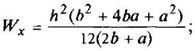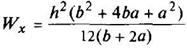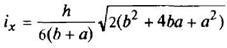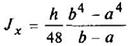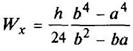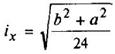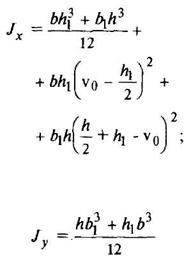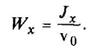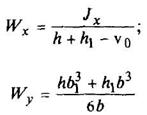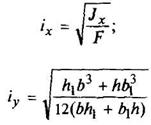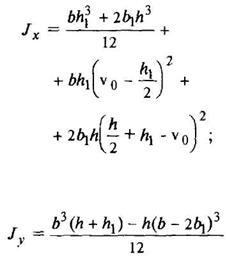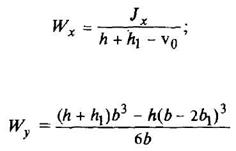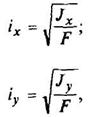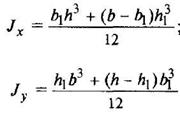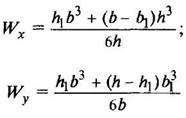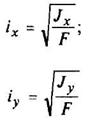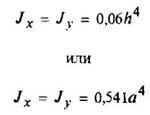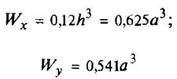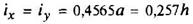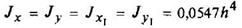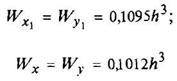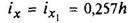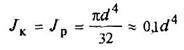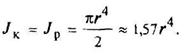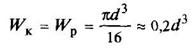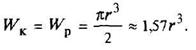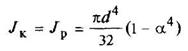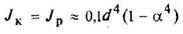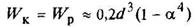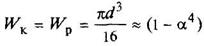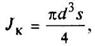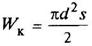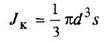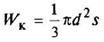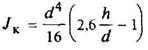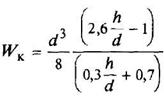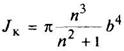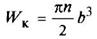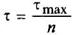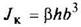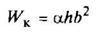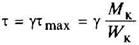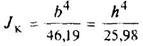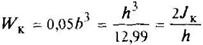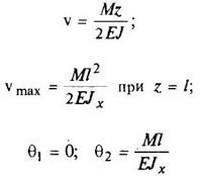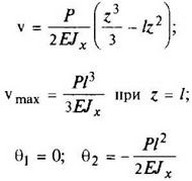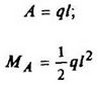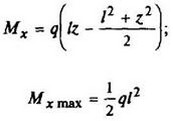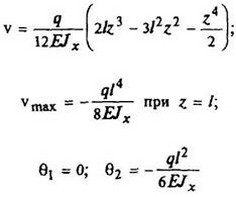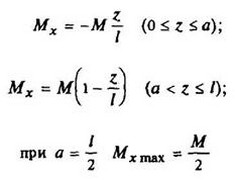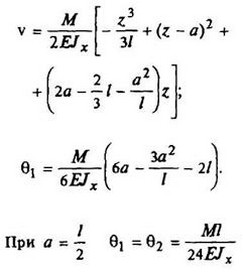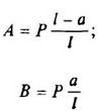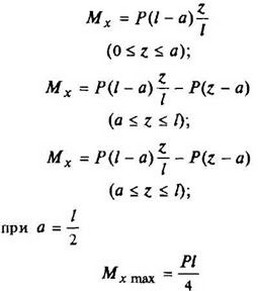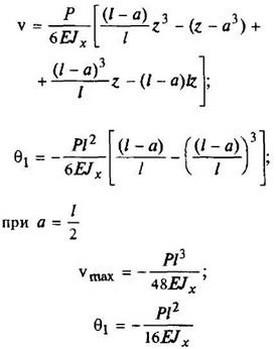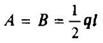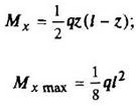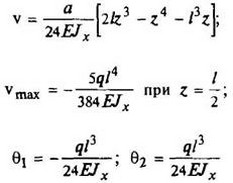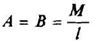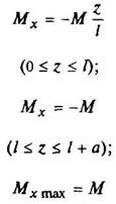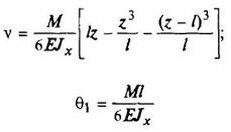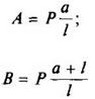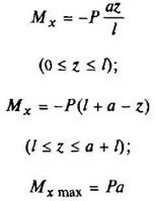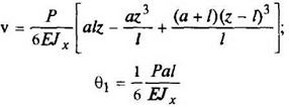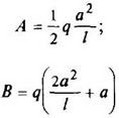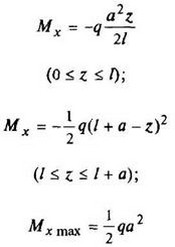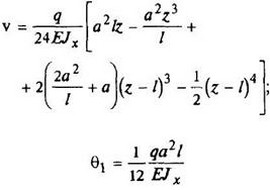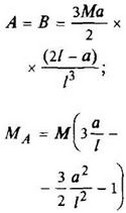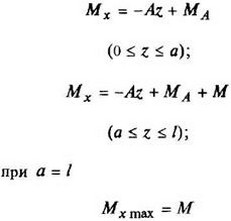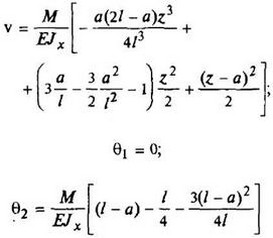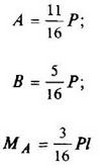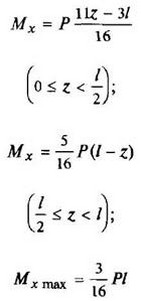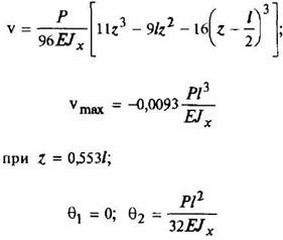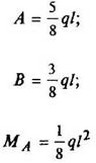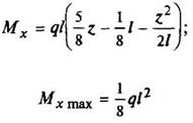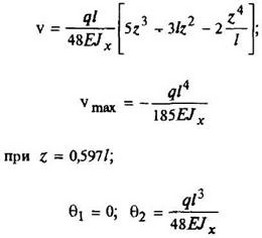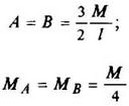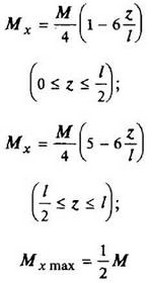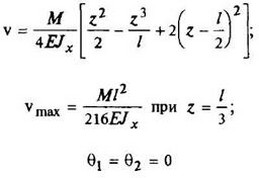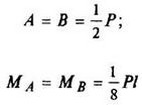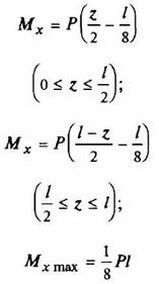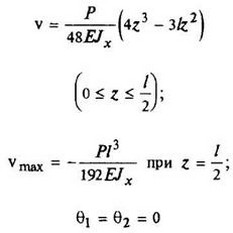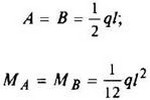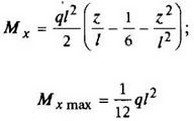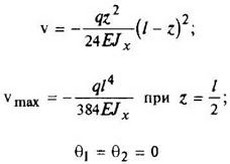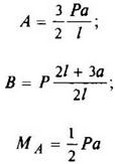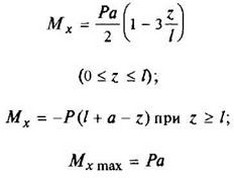0 руб
Оформить заказ6. Элементы сопротивления материалов
9. Значение модуля продольной упругости Е, модуля сдвига G и коэффициента Пуассона μ
(при температуре ~ 20 °С)
Материал | Модули, МПа | Коэффициент Пуассона, μ | |
Е | G | ||
Сталь | (1,86 ÷ 2,1) · 105 | (7,8 ÷ 8,3) · 104 | 0,25 - 0,33 |
Чугун: | |||
серый | (0,78 ÷1,47) · 105 | 4,4 · 104 | 0,23 - 0,27 |
серый модифицированный | (1,2 ÷1,6) · 105 | (5 ÷ 6,9) · 104 | – |
Медь техническая | (1,08- 1,3) · 105 | 4,8 · 104 | – |
Бронза: | |||
оловянная | (0,74 ÷ 1,22) · 105 | – | 0,32 - 0,35 |
безоловянная | (1,02 ÷ 1,2) · 105 | – | – |
Латунь алюминиевая | (0,98 ÷ 1,08) · 105 | (3,6 + 3,9) · 104 | 0,32 - 0,34 |
Алюминиевые сплавы | (0,69 ÷ 0,705) · 105 | 2,6 · 104 | 0,33 |
Магниевые сплавы | (0,4 ÷ 0,44) · 105 | – | 0,34 |
Никель технический | 2,5 · 105 | 7,35 · 104 | 0,33 |
Свинец технический | (0,15 ÷ 0,2) · 105 | 0,7 · 104 | 0,42 |
Цинк технический | 0,78 · 105 | 3,2 · 104 | 0,27 |
Кладка из кирпича | (0,24 ÷ 0,3) · 104 | – | – |
Бетон (при временном сопротивлении) (1-2 МПа) | (1,48 ÷ 2,25) · 104 | – | 0,16 - 0,18 |
Железобетон обычный: | |||
сжатые элементы | (1,8 ÷ 4,2) · 104 | – | – |
изгибаемые элементы | (1,07 ÷ 2,64) · 104 | – | – |
Древесина всех пород: | |||
вдоль волокон | (8,8 ÷ 15,7) · 104 | (4,4 ÷ 6,4) · 102 | – |
поперек волокон | (3,9 ÷ 9,8) · 104 | (4,4 ÷ 6,4) · 102 | – |
Фанера авиационная 1-го сорта: | |||
вдоль волокон | 12,7 · 103 | – | – |
поперек волокон | 6,4 · 103 | – | – |
Текстолит (ПТ, ПТК, ПТ-1) | (5.9 ÷ 9,8) · 103 | – | – |
Гетинакс | (9,8 ÷ 17.1) · 103 | – | – |
Винипласт листовой | 3.9 · 103 | – | – |
Стекло | (4,9 ÷ 5,9) · 104 | (2,05 ÷ 2,25) · 103 | 0,24 - 0,27 |
Органическое стекло | (2,8 ÷ 4,9) · 103 | – | 0,35 - 0,38 |
Бакелит без наполнителей | (1,96 ÷ 5,9) · 103 | (6,86 ÷ 20,5) · 102 | 0,35 - 0,38 |
Целлулоид | (1,47 ÷ 2,45) · 103 | (6,86 ÷ 9,8) · 102 | 0,4 |
Каучук | 0,07 · 104 | 2 · 103 | – |
Стеклопласт | 3,4 · 104 | (3,5 ÷ 3,9) · 103 | – |
(СВАМ1) вдоль волокон | |||
Капрон | (1,37 ÷ 1,96) · 103 | – | – |
Фторопласт Ф-4 | (4,6÷ 8,3) · 102 | – | – |
10. Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
(Моменты инерции J даны для главных центральных осей. Радиус инерции i = 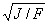 , где F - площадь сечения)
, где F - площадь сечения)
Форма поперечного сечения | Осевой момент инерции J, см4 | Момент сопротивления W, см3 | Радиус инерции I, см | ||||||||||||||||||
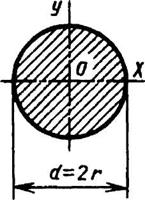
Круг
|
|
|
| ||||||||||||||||||
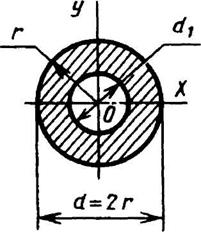
Кольцо
c = d1/d |
|
|
| ||||||||||||||||||
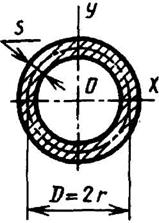
Тонкостенное кольцо
S ≤ D/10 |
|
|
| ||||||||||||||||||
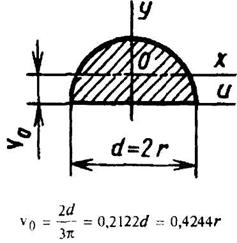
Полукруг
|
|
|
| ||||||||||||||||||
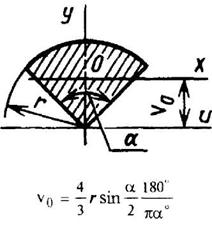
Круговой сегмент
|
|
|
| ||||||||||||||||||
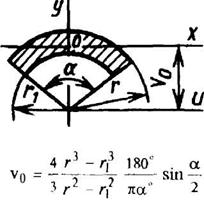
Круговой сектор
|
|
| |||||||||||||||||||
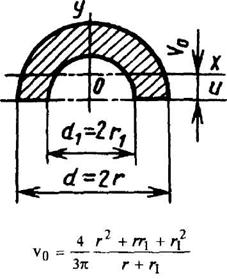
Круговое полукольцо
|
|
|
где F - площадь сечения | ||||||||||||||||||
Сектор кругового кольца
|
|
| |||||||||||||||||||
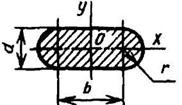
Профиль с симметричными закруглениями
r = d/2 |
|
| |||||||||||||||||||
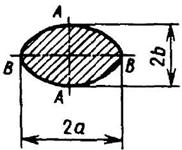
Эллипс
|
|
|
| ||||||||||||||||||
Квадрат
|
|
|
| ||||||||||||||||||
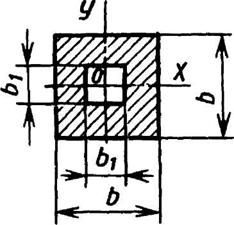
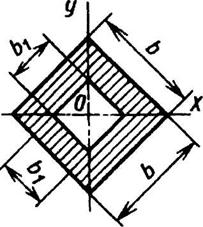
Полый квадрат
|
|
|
| ||||||||||||||||||
Полый тонкостенный квадрат
s < B/15 |
|
|
| ||||||||||||||||||
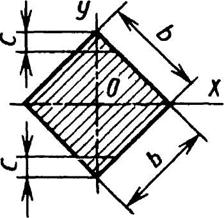
Квадрат, поставленный на ребро
|
|
Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С = 1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx = 0,124b3 | ix = iy = 0,289b | ||||||||||||||||||
Полый квадрат, поставленный на ребро
|
|
|
| ||||||||||||||||||
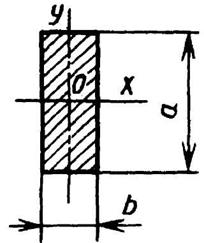
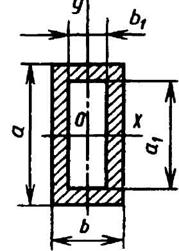
Прямоугольник
|
|
|
| ||||||||||||||||||
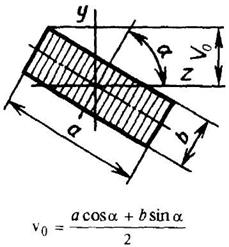
Прямоугольникповернутый
|
|
|
| ||||||||||||||||||
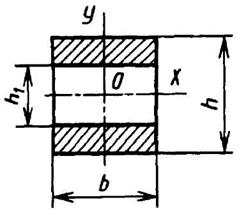
Полый прямоугольник
|
|
|
| ||||||||||||||||||
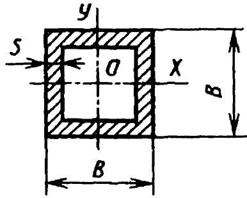
Полый тонкостенный прямоугольник
s < H/15 |
|
|
| ||||||||||||||||||
Сечение из двух равных прямоугольников
|
|
|
| ||||||||||||||||||
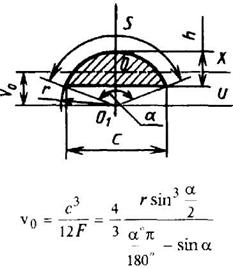
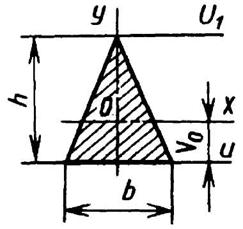
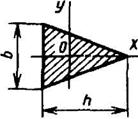
Треугольник
v0 = h/3 |
| При вычислении напряжения в вершине треугольника
при вычислении напряжения в точке основания
|
| ||||||||||||||||||
Поставленный на ребро треугольник
|
|
|
| ||||||||||||||||||
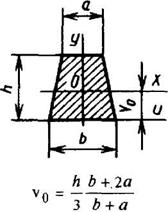
Трапеция
|
| При вычислении напряжений в точках верхнего основания
в точках нижнего основания
|
| ||||||||||||||||||
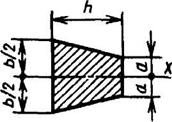
Трапеция
|
|
|
| ||||||||||||||||||
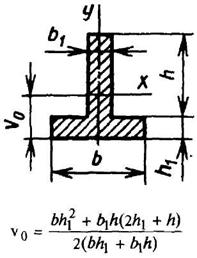
Тавр
|
| Для нижних волокон
Для верхних волокон
|
| ||||||||||||||||||
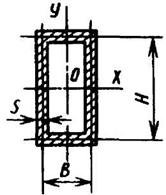
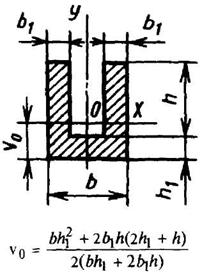
Корытное сечение
|
|
|
где F - площадь сечения | ||||||||||||||||||
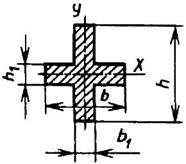
Крестообразное сечение
|
|
|
| ||||||||||||||||||
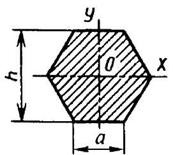
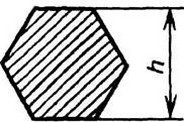
Правильный шестиугольник
|
|
|
| ||||||||||||||||||
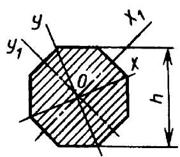
Правильный восьмиугольник
|
|
|
| ||||||||||||||||||
11. Геометрические характеристики жесткости и прочности для холодных сечений при кручении прямого бруса
Форма поперечного сечения бруса | Момент инерции при кручении Jк, см4 | Момент сопротивления при кручении Wк, см3 | Положение точки, в которой возникает наибольшее напряжение τ = Мк/Wк | ||||||||||||||||||
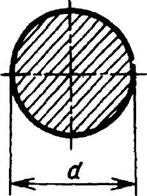
Круглое
|
или
Полярный момент инерции Jp = 2J |
или
Полярный момент сопротивления Wp = 2W | Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | ||||||||||||||||||
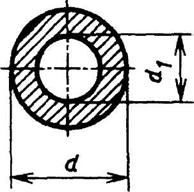
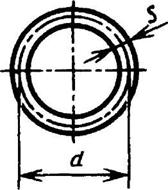
Кольцо
d1/d = a |
или
|
или
| Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | ||||||||||||||||||
Тонкостенное кольцо
s ≤ 0,1d |
d - средний диаметр |
| Все точки находятся в одинаковых условиях (приближенно) | ||||||||||||||||||
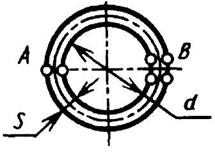
Незамкнутое тонкостенное кольцо
s < 0,1d |
|
| Наибольшее напряжение возникает в точках А. В точках В напряжение τ = 0 | ||||||||||||||||||
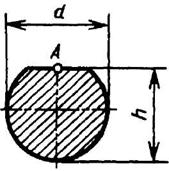
Круглое сечение с лыской
1 > h/d ≥ 0,5 |
|
| Наибольшее напряжение возникает в середине плоского среза (точка А). В углах τ = 0 | ||||||||||||||||||
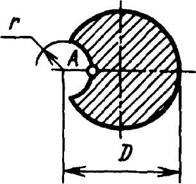
Круглое с круговым вырезом
D = 2R | Jк = K1R4 | Wк = R3/K2 | Наибольшее напряжение возникает по дну канавки (точка А) | ||||||||||||||||||
Значение коэффициентов К1 и K2 в зависимости от r/R | |||||||||||||||||||||
r/R | 0 | 0,05 | 0,1 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,5 | ||||||||||||
К1 | 1,57 | 1,56 | 1,56 | 1,46 | 1,22 | 0,92 | 0,63 | 0,38 | 0,07 | ||||||||||||
К2 | 0,64 | 1,22 | 1,22 | 1,23 | 1,31 | 1,52 | 1,91 | 2,63 | 7,14 | ||||||||||||
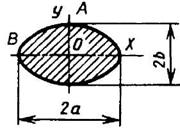
Сплошное эллиптическое
a/b = n ≥ 1 |
|
| Наибольшее напряжение в точках А. Напряжение в точках В
| ||||||||||||||||||
Прямоугольное
h/b ≥ 1 |
|
| Наибольшее напряжение возникает в серединах длинных сторон сечения (в точках А), в точках В напряжение
| ||||||||||||||||||
Значение коэффициентов α, β и γ в зависимости от h/b | |||||||||||||||||||||
h/b | 1,00 | 1,20 | 1,25 | 1,50 | 1,75 | 2,00 | 2,50 | 3,00 | 4,00 | 5,00 | 6,00 | 8,00 | 10,00 | Св. 10 | |||||||
α | 0,208 | 0,219 | 0,221 | 0,231 | 0,239 | 0,246 | 0,258 | 0,267 | 0,282 | 0,291 | 0,299 | 0,307 | 0,312 | 0,333 | |||||||
β | 0,141 | 0,166 | 0,172 | 0,196 | 0,214 | 0,229 | 0,249 | 0,263 | 0,281 | 0,291 | 0,299 | 0,307 | 0,312 | 0,333 | |||||||
γ | 1,00 | 0,93 | 0,91 | 0,86 | 0,82 | 0,79 | 0,77 | 0,75 | 0,74 | 0,74 | 0,74 | 0,74 | 0,74 | - | |||||||
Правильный шести- или восьмиугольник
| Jк = K'h2F. Для шестиугольника К' = 0,133. Для восьмиугольника К' = 0,130. F - площадь сечения | Wк = KhF. Для шестиугольника К = 0,217. Для восьмиугольника К = 0,233 | Наибольшие напряжения возникают в середине сторон В углах τ = 0 | ||||||||||||||||||
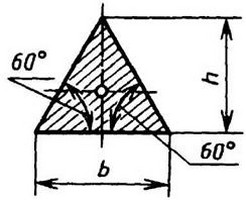
Равносторонний треугольник
|
|
| Наибольшие напряжения возникают в середине сторон В углах τ = 0 | ||||||||||||||||||
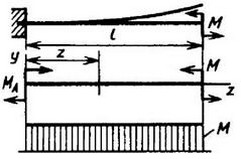
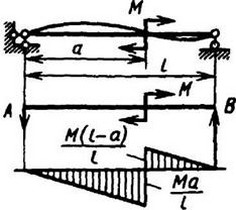
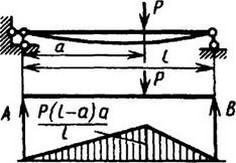
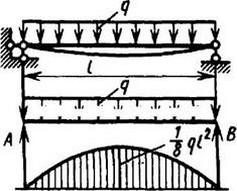
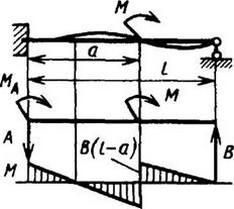
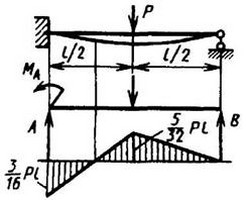
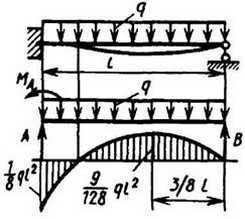
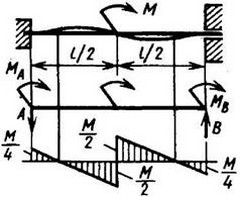
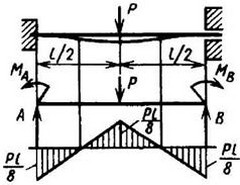
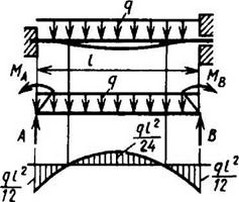
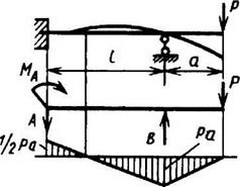
12. Расчетные данные для типовых балок постоянного сечения
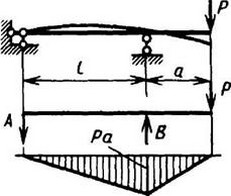
В таблице приведены: реакции А, МА (левой опоры) и В, MВ (правой опоры), выражение изгибающего момента Мх = Mх(z) в произвольном сечении с координатой z (начало координат совпадает с центром тяжести левого торца балки - см. схему 1), наибольший изгибающий момент Мх mах, уравнение упругой линии v - v(z); значения наибольшего прогиба vmax и углов поворота θ1 и θ2 соответственно крайнего левого сечения и крайнего правого сечения балки в радианах.
Для каждой балки представлены форма упругой линии и эпюра изгибающих моментов.
Внешние нагрузки обозначены: М - момент в вертикальной плоскости, совпадающей с осью бруса z; Р - сосредоточенная сила и q -интенсивность распределенной нагрузки, действующие в той же плоскости; Е - модуль продольной упругости; Jx - осевой момент инерции поперечного сечения относительно оси х.
Схема закрепления балки, форма упругой линии. Эпюра изгибающих моментов | Реактивные силы и моменты опор | Изгибающий момент в произвольном сечении, наибольший изгибающий момент | Уравнение упругой линии, наибольший прогиб, углы поворота крайних сечений балки |
Схема 1
| MA = M | Mx = M; Mx max = M |
|
Схема 2
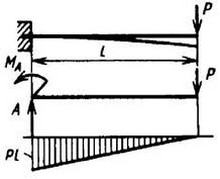
| A = P; MA = Pl | Mx = P(z - l); Mx max = Pl |
|
Схема 3
|
|
|
|
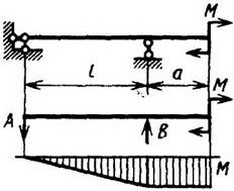
Схема 4
| A = B = M/l |
|
|
Схема 5
|
|
|
|
Схема 6
|
|
|
|
Схема 7
|
|
|
|
Схема 8
|
|
|
|
Схема 9
|
|
|
|
Схема 10
|
|
|
|
Схема 11
|
|
|
|
Схема 12
|
|
|
|
Схема 13
|
|
|
|
Схема 14
|
|
|
|
Схема 15
|
|
|
|
Схема 16
|
|
|
|